
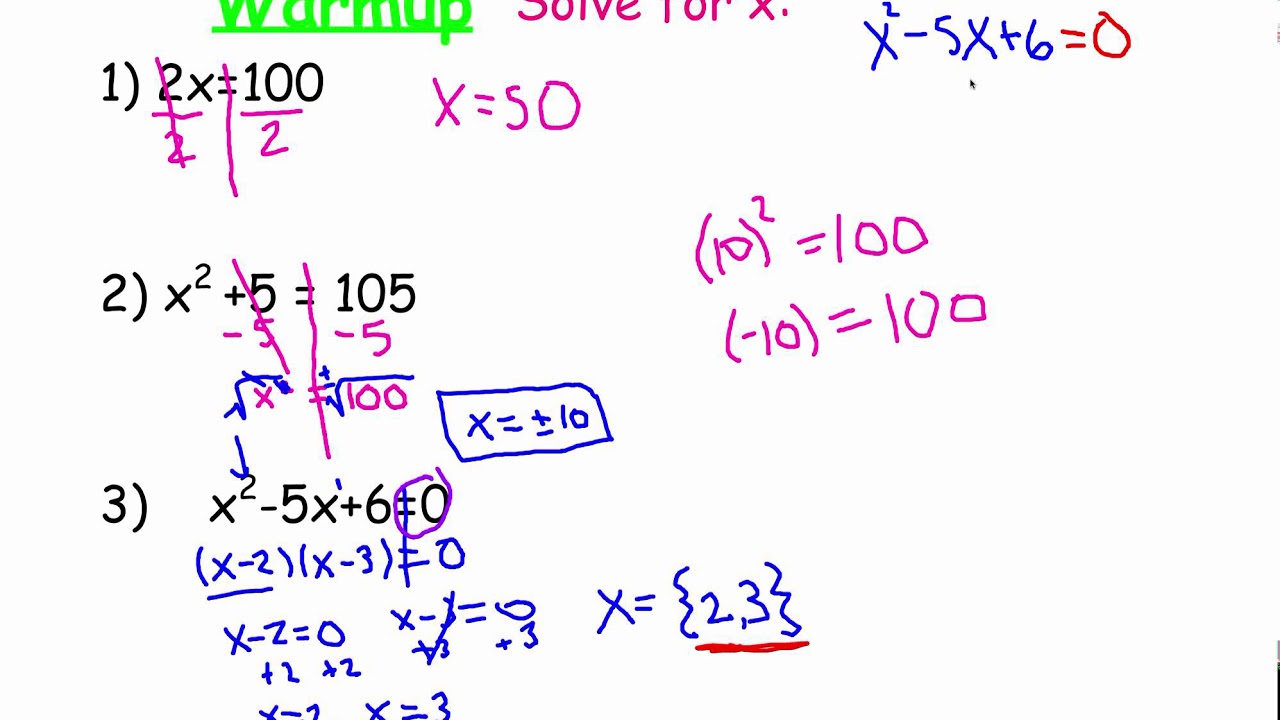
Note that any value that makes either or zero, will make their product zero. Why is this a quadratic equation This is a product of two expressions that is equal to zero. Solving Quadratic Equations by Factoring when Leading Coefficient is not 1 - Procedure (i) In a quadratic equation in the form ax2 + bx + c 0, if the leading coefficient is not 1, we have to multiply the coefficient of x2 and the constant term. The method of solving quadratic equations by factoring depends whether the standard form equation is given as a simple or as a complex trinomial and whether.
#SOLVING QUADRATIC EQUATIONS BY FACTORING PLUS#
We could write this as x squared minus 14x plus 49 is equal to 0. Thats the best way to solve a quadratic equation. First get it into factored form, set it equal to zero, and then separate your two factors, make each factor equal to zero and solve for x. Solving factored quadratic equations Suppose we are asked to solve the quadratic equation. Once again, whenever you see anything like this, get all of your terms on one side of the equation and get a 0 on the other side. This is how you're going to go about solving quadratic equations by factoring.
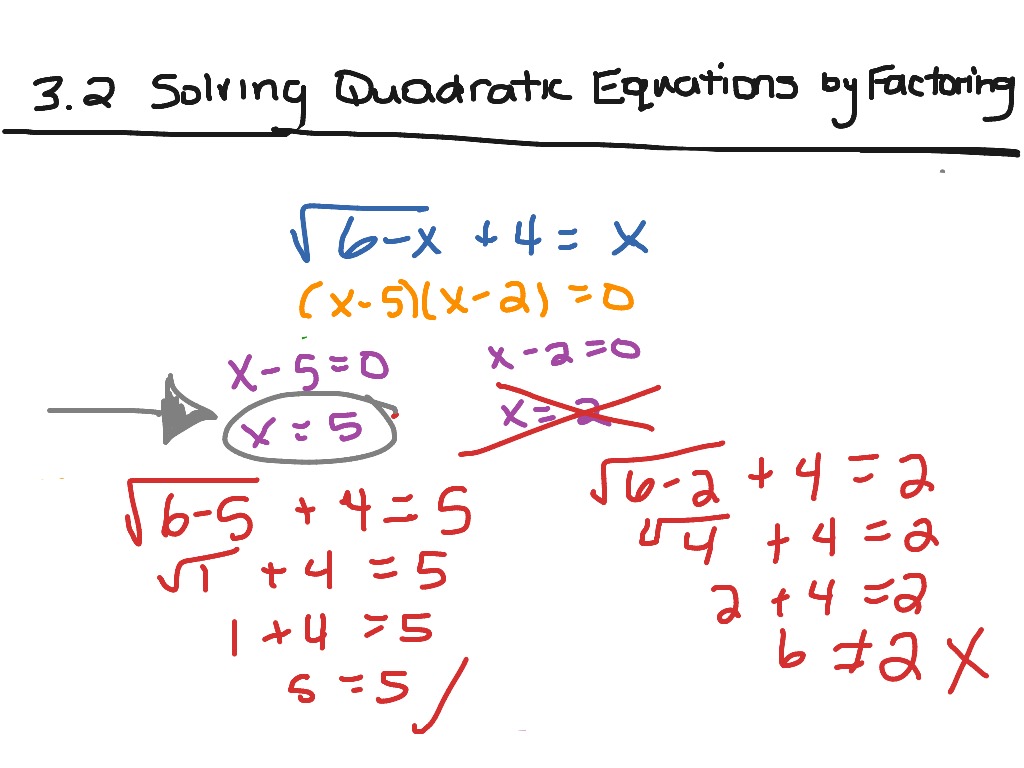
Subtract 4 from both sides and I'm going to get my solutions x=-4 or x=-1. If a times b is zero, then either a=0 or b=0. However, the method only works for the most basic equations. What that tells me is that x+4=0 or x+1=0. The example above shows that it is indeed easy to solve quadratics by factoring method. I have this binomial multiplied by that binomial, I have a product and the answer is zero. Factoring can be considered as the reverse process of the multiplication distribution. Two positive integers are 3 units apart on a number line. Factoring quadratic equations consists of rewriting the quadratic equation to form a product of its factors. Two negative integers are 8 units apart on the number line and have a product of 308. Which is a solution to the equation (x 2) (x + 5) 18. But no need to worry, we include more complex examples in the next section. Their teacher states that after the two new squares are formed, one should have a side length two units greater than the other. We simply must determine the values of r1 r1 and r2 r2. Now think about the zero products property. In these cases, solving quadratic equations by factoring is a bit simpler because we know factored form, y (x-r1) (x-r2) y (x r1)(x r2), will also have no coefficients in front of x x. An equation can be solved by expressing it as a product of multiple factors that equate to zero. And let's just say instead of y right there I stuck a zero, either because I was trying to solve or because I was trying to find the x intercepts. I factored it, that was my factored form. Let's just say I have the equation that looks like this y=x+4 times x+1. In this algebra lesson, we will discuss how factoring can be used to solve Quadratic Equations, which are equations of the form: ax2 + bx + c 0 where a, b and. It's the same idea with quadratic equations. Like a product means multiplying and if you have two numbers multiplied together and your answer is zero, then one of those numbers has to be zero. The zero product property says that if a times b is zero then either a=0 or b=0 and that makes sense. Step 2: Rewrite the middle with those numbers: Step 3: Factor. This page will try to solve a quadratic equation by factoring it first. There's a important property we have about zero that's called the zero product property. Step 1: Find two numbers that multiply to give ac (in other words a times c), and add to give b. So one way many students choose to go about this is by using factoring techniques.īefore we get into that though, it's important to think about some stuff you already know about zero. If you are on the foundation course, any quadratic. Quadratics are algebraic expressions that include the term, x2, in the general form. Factoring Quadratic Equations when a 1 Step 1: Write the equation in the general form Step 2: Multiple Step 3: Determine the factor pairs of Step 4. The correct answer is \(\ m=-8\) or 3.When you're asked to solve a quadratic equation, what that means is you're trying to find what x values make that equation true. Solving Quadratic Equations by Factorising. However, the original equation is not equal to 0, it’s equal to 48. \( \newcommand+10 m\) as \(\ 2 m(m+5)\) and then set the factors equal to 0, as well as making a sign mistake when solving \(\ m+5=0\).


 0 kommentar(er)
0 kommentar(er)
